[最も選択された] trigonometric identities tan^2 296912-Trig identities tan^2 theta

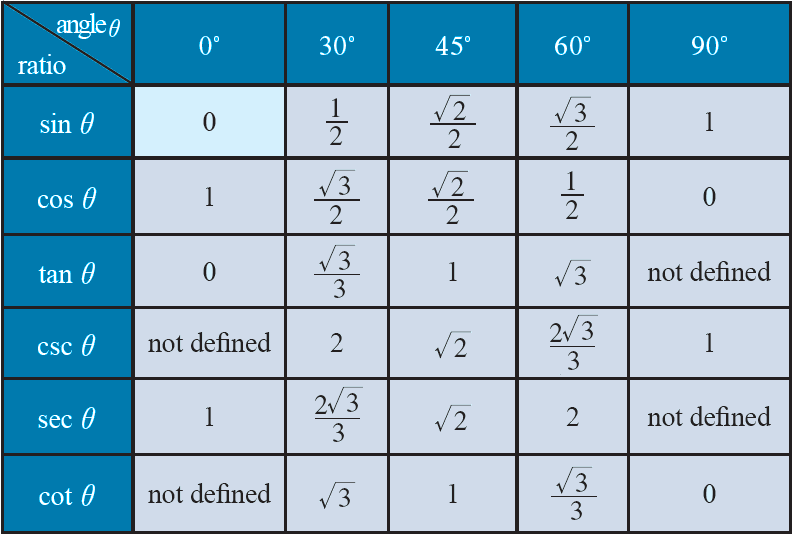
4/5/21 · 5 Prove that tan 3x tan 2 tan = tan 3x – tan 2 – tan 6 Calculate general solution of the equation tan 2 θ (2 – √6) tan θ – √2 = 0 7 In a triangle, the length of the two larger sides are 12 cm and 7 cm, respectively If the angles of the triangle are in arithmetic progression, then what is the length of the third side in cm?D is the differential operator, int is the integration operator, C is the constant of integration Identities tan x = sin x/cos x equation 1 cot x = cos x/sin x equation 2 sec x = 1/cos x equation 3 csc x = 1/sin x equation 411/9/ · Trigonometric Identities Sine, tangent, cotangent and cosecant in mathematics an identity is an equation that is always true Meanwhile trigonometric identities are equations that involve trigonometric functions that are always true This identities

Trigonometric Identities

Trig identities tan^2 theta

Trig identities tan^2 theta-Pythagorean Trigonometric Identities For any theta, sin 2 θ cos 2 θ = 1 sin 2 θ cos 2 θ = 1 1 cot 2 θ = csc 2 θ 1 cot 2 θ = csc 2 θ tan 2 θ 1 = sec 2 θ tan 2 θ 1 = sec 2 θ Note that this need not me memorized, connect these to the Pythogoras theoremHigh School Math Solutions – Trigonometry Calculator, Trig Identities In a previous post, we talked about trig simplification Trig identities are very similar to this concept

A Trig Identity

$$tan(2θ)={2 tan(θ)}/{1– tan^2(θ)}$$ Additional Trig Identities These three categories of trig identities are used less often You should look through them to make sure you understand them, but they typically don't need to be memorized HalfAngle Identities These are inversions of the doubleangle identities $$sin2(θ) = {1/2}(1cos (2θ))$$12/8/ · Conditional trigonometrical identities We have certain trigonometric identities Like sin 2 θ cos 2 θ = 1 and 1 tan 2 θ = sec 2 θ etc Such identities are identities in the sense that they hold for all value of the angles which satisfy the given condition among them and they are called conditional identitiesA trigonometric equation is an equation that involves a trigonometric function or functions When we solve a trigonometric equation we find a value for the trigonometric function and then find the angle or angles that correspond to that particular trigonometric function 2 Some important identities derived from a right­angled triangle

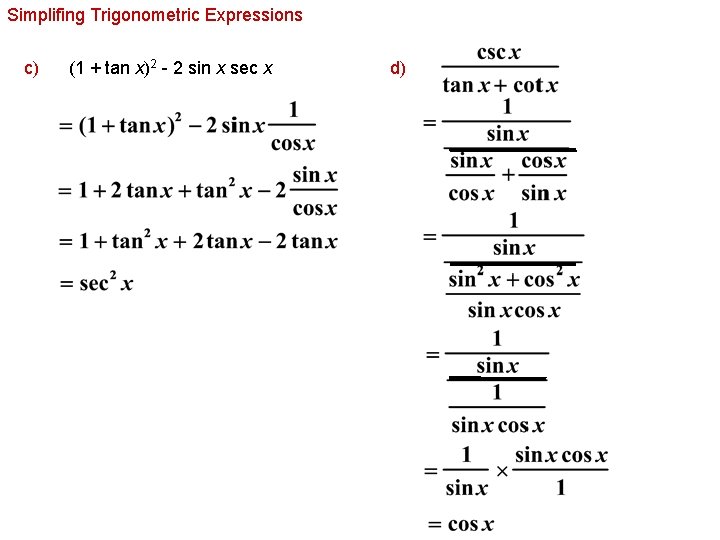
3/26/ · Solving trigonometric functions often requires trigonometric identities A trig identity is an equality that is true for every valueChapter 4 Trigonometry Emphasize the value and importance of making sketches, where appropriate It is very important for learners to understand that it is incorrect to apply the distributive law to the trigonometric ratios of compound angles and that \(\cos (\alpha \beta) \ne \cos \alpha \cos \beta\)θ = ( 1 ) ( 1 − ) cos 2 ⁡ θ − 1 = Here are some useful tips for proving identities Change all trigonometric ratios to sine and cosine Choose one side of the equation to simplify and show that it is equal to the other side Usually it is better to

Trigonometric Identities and Formulas Below are some of the most important definitions, identities and formulas in trigonometry Trigonometric Functions of Acute Angles sin X = opp / hyp = a / c , csc X = hyp / opp = c / a tan X = opp / adj = a / b , cot X = adj / opp = b / a cos X = adj / hyp = b / c , sec X = hyp / adj = c / b ,Trigonometry Identity tan^2 (x) 1 = sec^2 (x) Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device Up next in 81/17/ · The trigonometric identities act in a similar manner to multiple passports—there are many ways to represent the same trigonometric expression Just as a spy will choose an Italian passport when traveling to Italy, we choose the identity that applies to the given scenario when solving a trigonometric equation

List Of Trigonometric Identities Wikipedia

Solved Proving Trigonometric Identities Q1 Prove That Sin Chegg Com

2/17/19 · In Trigonometry, different types of problems can be solved using trigonometry formulas These problems may include trigonometric ratios (sin, cos, tan, sec, cosec and cot), Pythagorean identities, product identities, etc Some formulas including the sign of ratios in different quadrants, involving cofunction identities (shifting angles), sum & difference identities, double angle identities6/18/ · There are three basic trigonometric identities in class 10 which relate the trigonometric ratios mutually The three basic trigonometric identities learned in class 10 are Sin 2 A Cos 2 A = 1 Sec 2 A = 1 Tan 2 A Cosec 2 A = 1 Cot 2 A These identities can be derived by considering the right triangle The right triangle is subjected to the Pythagorean theoremTrigonometric Identities From Math Wiki Jump to navigation Jump to search Contents 1 List of identities;

6 1 2 Trigonometric Identities

Summary Of Trigonometric Identities

Free math lessons and math homework help from basic math to algebra, geometry and beyond Students, teachers, parents, and everyone can find solutions to their math problems instantlySimplify\\sin^2 (x)\cos^2 (x)\sin^2 (x) simplify\\tan^4 (x)2\tan^2 (x)1 simplify\\tan^2 (x)\cos^2 (x)\cot^2 (x)\sin^2 (x) trigonometricsimplificationcalculator enPythagorean Trig Identities Pythagoras Trig Identities are the trigonometric identities which actually the true representation of the Pythagoras Theorem as trigonometric functions So, these identities help us to fundamentally decide the relationship between different sine, cosine, and tan trigonometric function

Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities

While You Wait Trigonometric Identities And Equations Section

Basic Trig Identities tan x = sin x/cos x Equation 1 cot x = cos x/sin x Equation 2 sec x = 1/cos x Equation 3 csc x = 1/sin x Equation 4 cot x = 1/tan x Equation 5 sin 2 x cos 2 x = 1 Equation 6 tan 2 x 1 = sec 2 x Equation 7 1 cot 2 x = csc 2 x Equation 8 cos (x y) = cos x cos y sin x sin y Equation 93/12/21 · Trigonometric Identities Each of the six trig functions is equal to its cofunction evaluated at the complementary angle Periodicity of trig functions Sine, cosine, secant, and cosecant have period 2π while tangent and cotangent have period π Identities for negative anglesExamples prove\\tan^2 (x)\sin^2 (x)=\tan^2 (x)\sin^2 (x) prove\\cot (2x)=\frac {1\tan^2 (x)} {2\tan (x)} prove\\csc (2x)=\frac {\sec (x)} {2\sin (x)} prove\\frac

Trigonometry Identities And Equations Ppt Download

Summary Of Trigonometric Identities

Trigonometric Identities List There are various identities in trigonometry which are used for many trigonometric problems Let us see all the fundamental trigonometric identities here Reciprocal Identities Sin θ = 1/Csc θ or Csc θ = 1/Sin θ;Cos θ = 1/Sec θ or Sec θ = 1/Cos θ;Without using trigonometrical tables, evaluate cosec 2 57° – tan 2 33° cos 44° cosec46° – \(\sqrt{2}\)cos45° – tan 2 60° Solution Trigonometrical Identities Exercise 21D – Selina Concise Mathematics Class 10 ICSE Solutions Question 1 Solution Question 2 Solution Question 3 Solution Question 4 Solution Question 5

Trigonometric Identity Example Proof Involving Sin Cos And Tan Video Khan Academy

Trig Identities All List Of Trigonometric Identities Learn Trigonometry

Proving a trigonometric identity refers to showing that the identity is always true, no matter what value of x x x or θ \theta θ is used Because it has to hold true for all values of x x x, we cannot simply substitute in a few values of x x x to "show" that they are equal It is possible that both sides are equal at several values (namely when we solve the equation), and we might falsely12/23/16 · What are the cofunction identities and reflection properties for trigonometric functions?7/10/18 · Trigonometric identities are used to manipulate the trigonometric equations of some specific forms In this video, the Pythagorean identities and the way they are derived are shown In mathematics, there are numerous logarithmic identities

Tangent Half Angle Formula Wikipedia

What Is The Formula Of Tan2x Quora

If #sec theta = 4#, how do you use the reciprocal identity to find #cos theta#?What is the pythagorean identity?3/14/14 · in the previous video we explored how the cosine and sines of angles relate when we essentially take the terminal ray of the angle and we reflect it about the X or the y axis or or both axes what I want to do in this video is think a little bit about the tangent of these different angles so just as a little bit of a reminder we know that the tangent of theta is equal to the sine of an angle

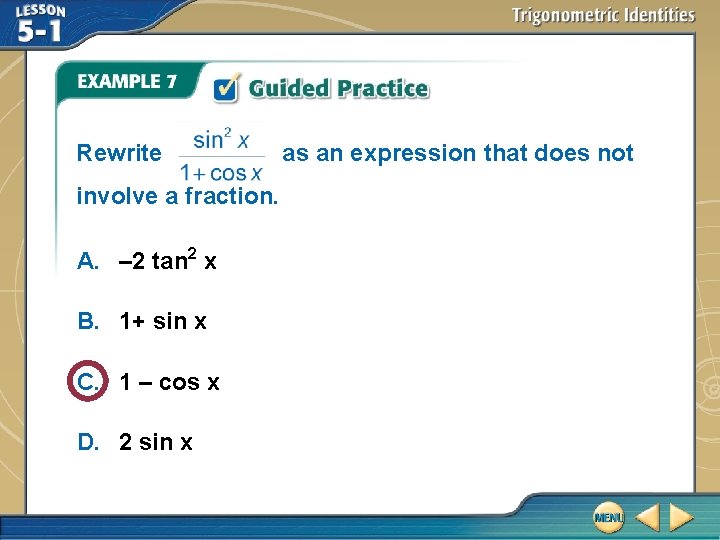
Lesson 5 1 Trigonometric Identities Fiveminute Check Over

Solved Use The Trigonometric Identities To Simplify The E Chegg Com

A) sin 2 acos 2 a = 1 b) sin a = tan a * cos a c) 1 cot 2 a = csc 2 a d) 1 sec 2 a = tan 2 a Question 2 Which of the following is an identity?Trigonometric Identities 43 Introduction A trigonometric identity is a relation between trigonometric expressions which is true for all values of the variables (usually angles) There are a very large number of such identities In this Section we discuss only the most important and widely used Any engineer using trigonometry in an applicationProving Trigonometric Identities Calculator online with solution and steps Detailed step by step solutions to your Proving Trigonometric Identities problems online with our math solver and calculator Solved exercises of Proving Trigonometric Identities

Important Trigonometric Identiti

Example 1 Verify A Trigonometric Identity The Left Hand Side Of This Identity Is More Complicated So Transform That Expression Into The One On The Right Ppt Download

Trigonometry (from Greek trigōnon, "triangle" and metron, "measure") is a branch of mathematics that studies relationships between side lengths and angles of triangles The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies The Greeks focused on the calculation of chords · Explanation Change to sines and cosines then simplify 1 tan2x = 1 sin2x cos2x = cos2x sin2x cos2x but cos2x sin2x = 1 we have ∴ 1 tan2x = 1 cos2x = sec2xMultiple choice questions on trigonometric identities with answers at the bottom of the page Questions with Answers Question 1 Which of the following is not an identity?

Powers Of Trigonometric Functions

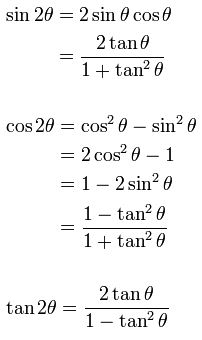
Trigonometric Identities Definition Rules Examples S Sigma Tricks

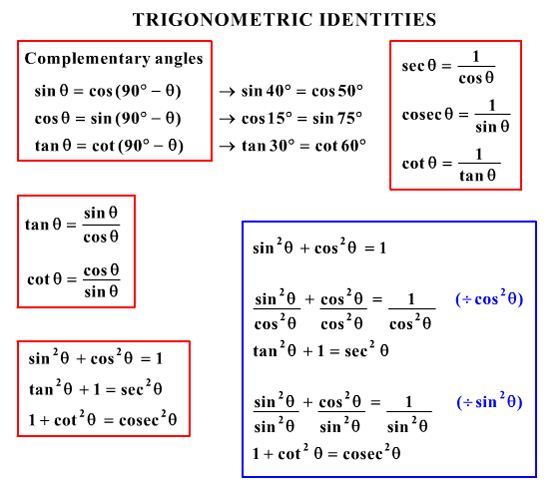
Trig Equations and Identities wwwnaikermathscom 4 (a) Given that sin q = 5 cos q, find the value of tan q (1) (b) Hence, or otherwise, find the values of q in the interval 0 £ q < 360° for which sin q = 5 cos q, giving your answers to 1 decimal place (3) June 06 Q6 5 (a) Show that the equation 3 sin2 q – 2 cos2 q = 1 can be written asIdentities expressing trig functions in terms of their complements cos t = sin(/2 – t) sin t = cos(/2 – t) cot t = tan(/2 – t) tan t = cot(/2 – t) csc t = sec(/2 – t) sec t = csc(/2 – t) Periodicity of trig functions Sine, cosine, secant, and cosecant have period 2List of identities Given two functions f and g, we say f = g if f(x) = g(x) for all every x in the domain of both f and g

Trig Identities Bingo Card

Trigonometric Identities Solutions Examples Videos

Tan θ = 1/Cot θ or Cot θ = 1/Tan θ;Math2org Math Tables Trigonometric Identities sin (theta) = a / c csc (theta) = 1 / sin (theta) = c / a cos (theta) = b / c sec (theta) = 1 / cos (theta) = c / b tan (theta) = sin (theta) / cos (theta) = a / b cot (theta) = 1/ tan (theta) = b / a sin (x) = sin (x)The half‐angle identity for tangent can be written in three different forms In the first form, the sign is determined by the quadrant in which the angle α/2 is located Example 5 Verify the identity Example 6 Verify the identity tan (α/2) = (1 − cos α)/sin α Example 7 Verify the identity tan (α − 2) = sin π/(1 cos α)

14 2 Trigonometric Identities

Trig Identities Hsn Forum

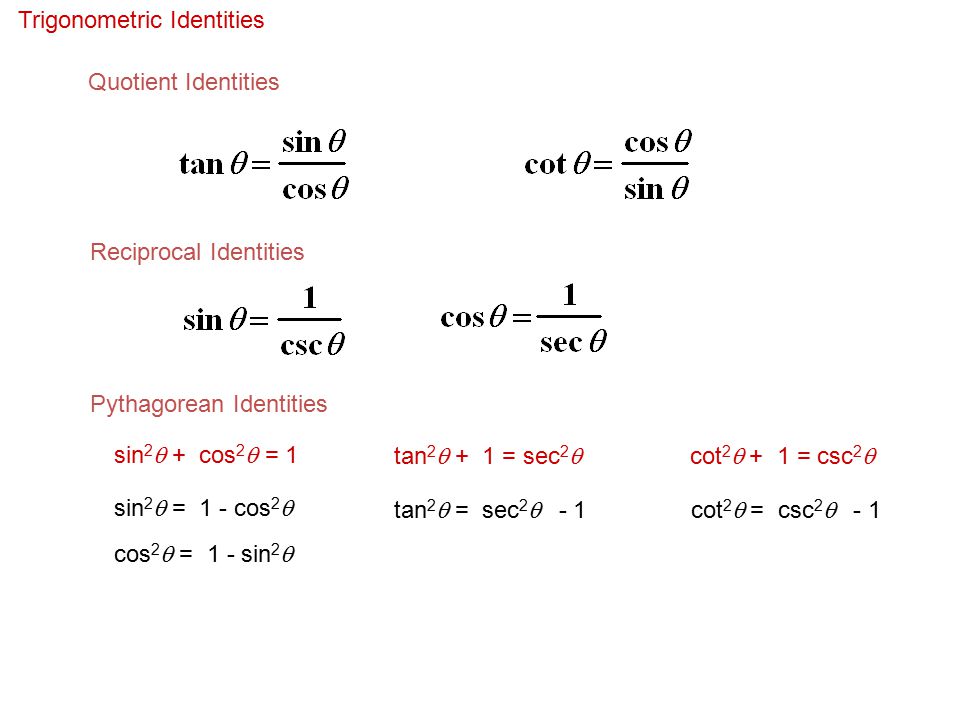
TRIGONOMETRIC IDENTITIES Reciprocal identities sinu= 1 cscu cosu= 1 secu tanu= 1 cotu cotu= 1 tanu cscu= 1 sinu secu= 1 cosu Pythagorean Identities sin 2ucos u= 1 1tan2 u= sec2 u 1cot2 u= csc2 u Quotient Identities tanu= sinu cosu cotu= cosu sinu CoFunction Identities sin(ˇ 2 u) = cosu cos(ˇ 2 u) = sinu tan(ˇ 2 u) = cotu cot(ˇ 2 u8/8/13 · tan²θ = sin²θ cos²θ = 1 That is wrong tan²θ = sin²θ/cos²θ Secondly, the identity is tan²θ 1 = sec²θ, not tan²θ 1 Maybe this proof will be easier to follow tan²θ 1 = sin²θ/cos²θ 1 = sin²θ/cos²θ cos²θ/cos²θ = (sin²θ cos²θ)/cos²θ //sin²θ cos²θ =Legend x and y are independent variables, ;

Derivatives Of Trigonometric Functions

How To Use Double Angle Identities Studypug

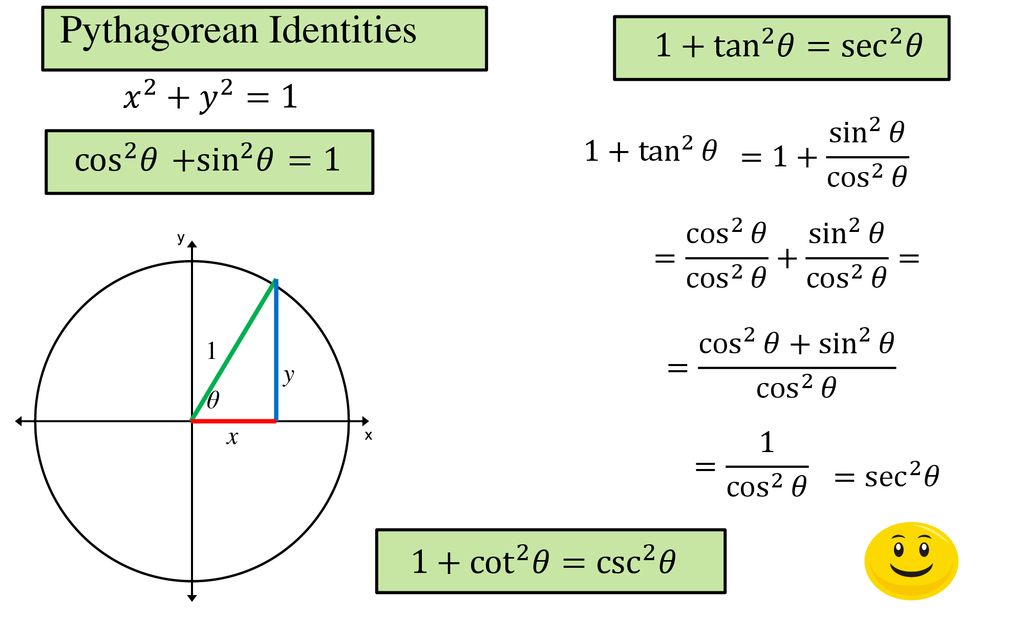
The evenodd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle and determine whether the identity is odd or even EvenOdd Identities tan(−θ)=−tanθ cot(−θ)=−cotθ tan ⁡The three identities are latex\cos^2 t \sin^2 t = 1/latex, latex1 \tan^2 t = \sec^2 t/latex, and latex1 \cot^2 t = \csc^2 t/latex The Pythagorean identities can be used to simplify problems by transforming trigonometric expressions, or writing them in terms of other trigonometric functionsTrigonometric Identities Pythagoras's theorem sin2 cos2 = 1 (1) 1 cot2 = cosec2 (2) tan2 1 = sec2 (3) Note that (2) = (1)=sin 2 and (3) = (1)=cos Compound

11 Basic Trigonometric Identities An Identity Is An Equation That Is True For All Defined Values Of A Variable We Are Going To Use The Identities To Ppt Download

A Trig Identity

Tangent Identities

Trigonometric Identities

2sinxcosx Identity Gamers Smart

Integrate Sec 2x Method 1

Tangent Half Angle Formula Wikipedia

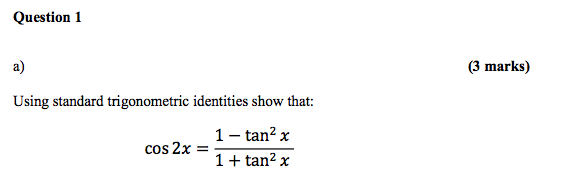
Solved A Using Standard Trigonometric Identities Show Th Chegg Com

Basic Trigonometric Identities And Equations Trigonometric Identities Quotient

Important Trigonometric Identiti

Answered O Trigonometric Identities And Bartleby

How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic

1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube

Solved Using Standard Trigonometric Identities Show That Chegg Com

Trigonometric Identities Sin 2 X Cos 2 X Tan 2 X Youtube

How I Remember Trig Identities Part 2 Beyond Solutions

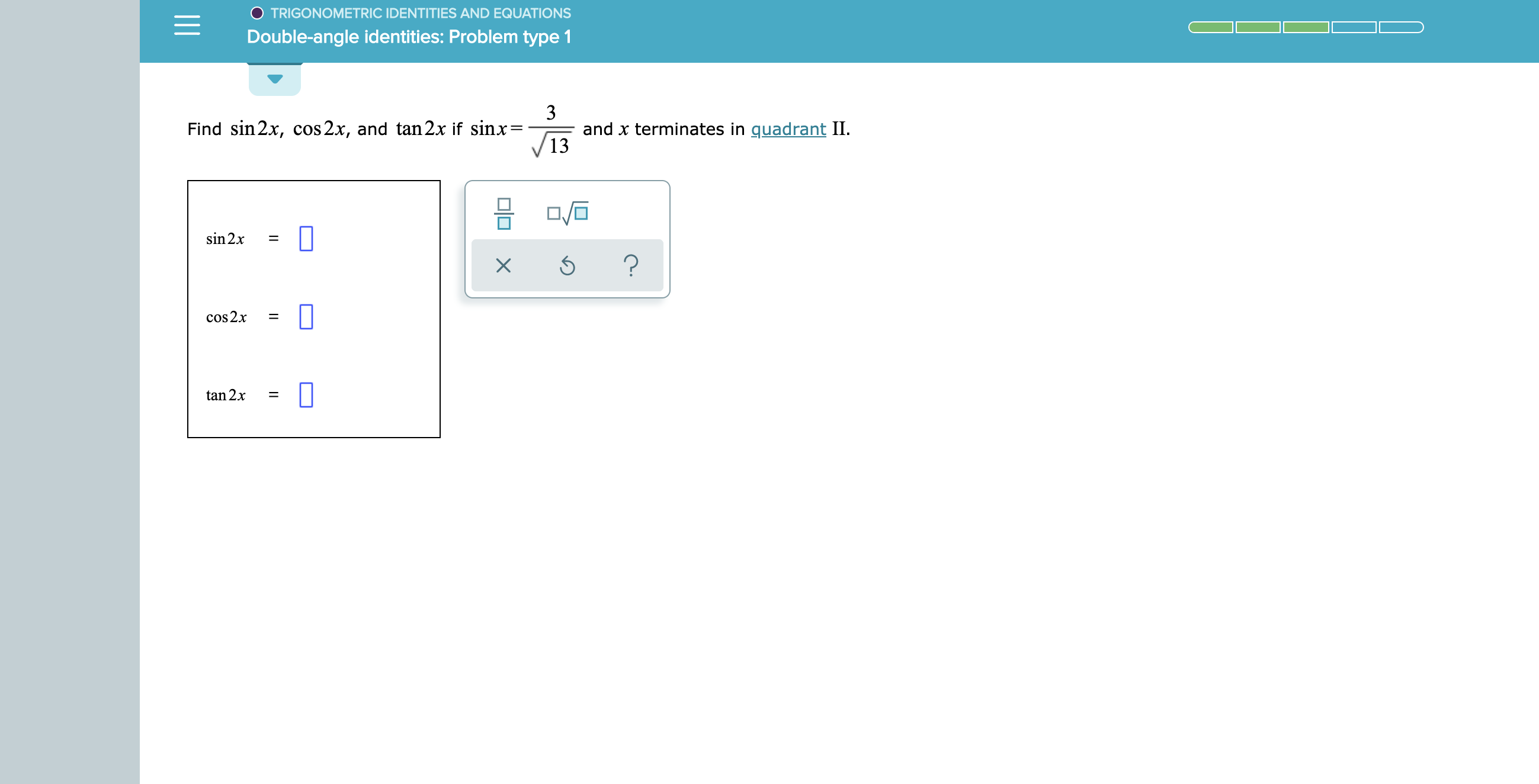
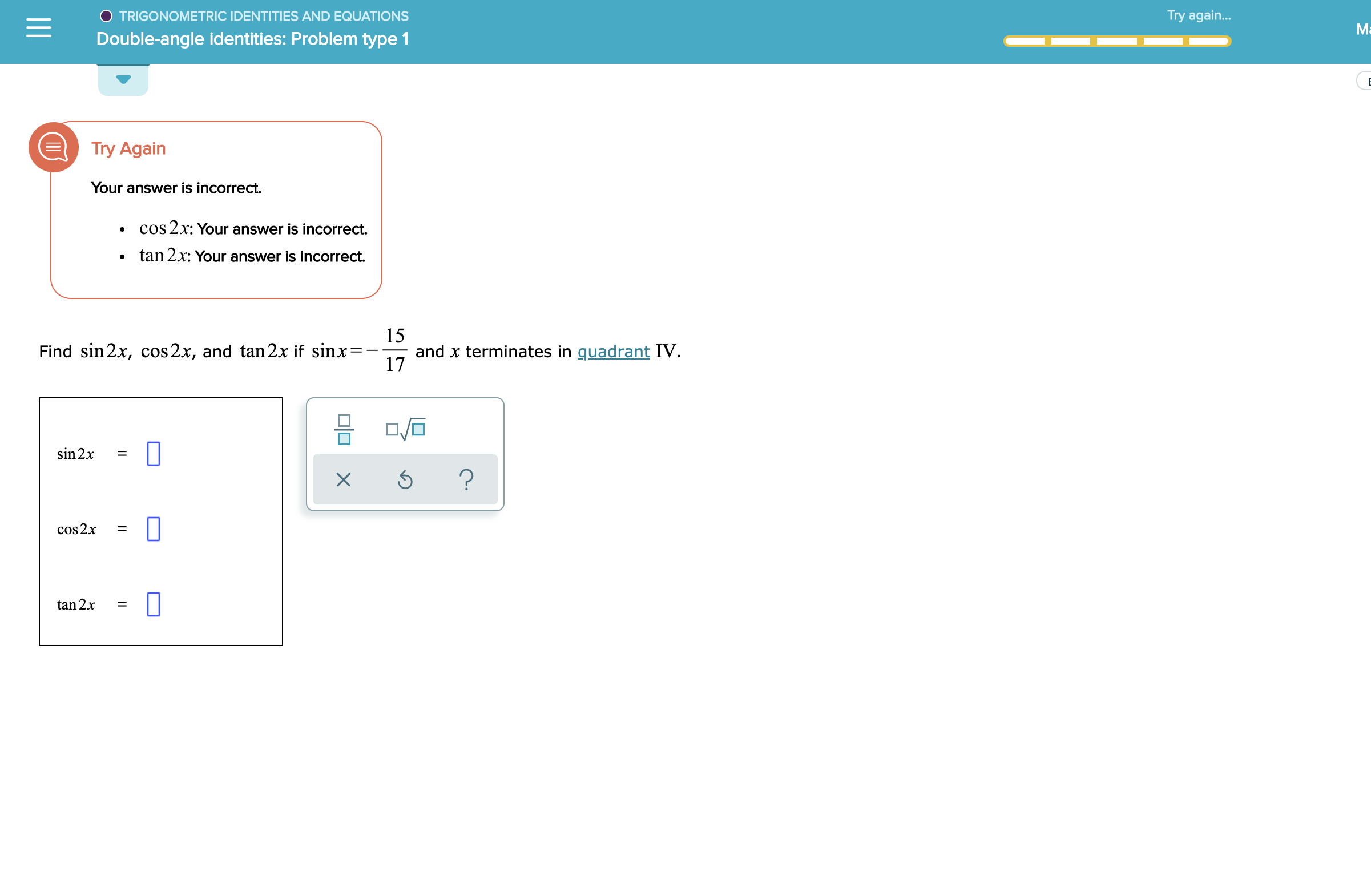
Answered Trigonometric Identities And Equations Bartleby

How Do You Verify The Identity Tan2theta 2 Cottheta Tantheta Socratic

Double Angle And Multiple Angle Identities

Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube

Summary Of Trigonometric Identities

Trigonometric Identities And Examples With Worksheets

Verify The Trigonometric Identity 1 1 Sin 2 X 1 Tan 2 X In 21 Identity Sins Tan

Quotient Identities Evaluating Tangent And Cotangent Functions Youtube

Trigonometric Identities And Equations Ppt Download

Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube

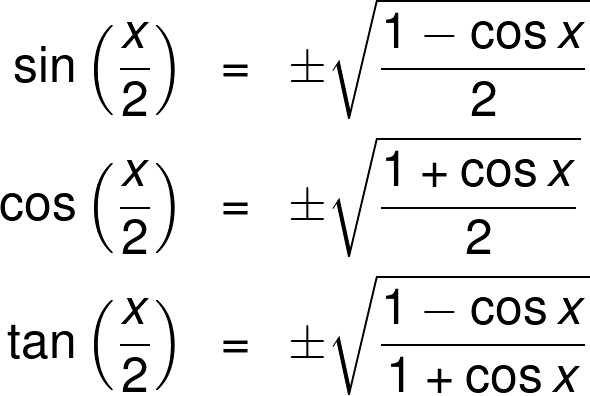
Half Angle Calculator

14 2 Trigonometric Identities

Trigonometric Identities

What Is The Formula Of Tan2x Quora

Worksheet On Finding The Unknown Angle Using Trigonometric Identities

How To Solve Tan 2y Sec 2y Tan 4y Tan 2y Socratic

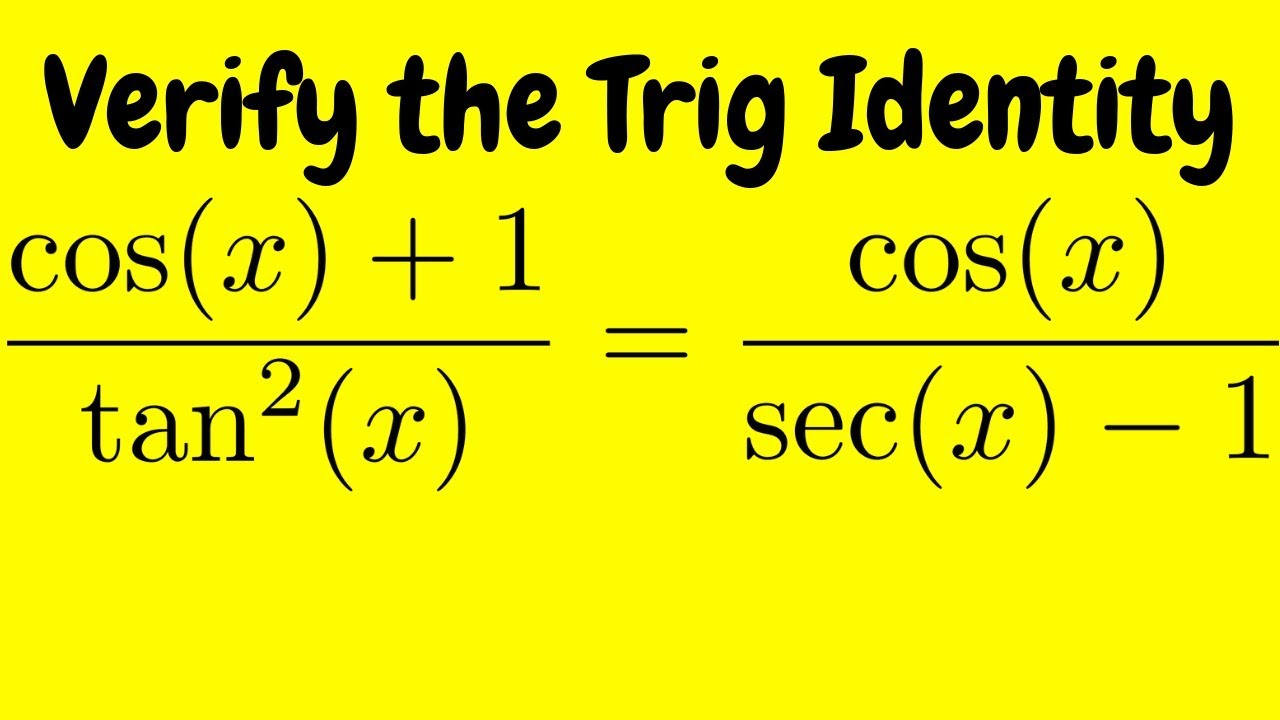
Verifying A Trigonometric Identity Cos X 1 Tan 2 X Cos X Sec X 1 Youtube

14 2 Trigonometric Identities

Tangent Identities

How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube

Art Of Problem Solving

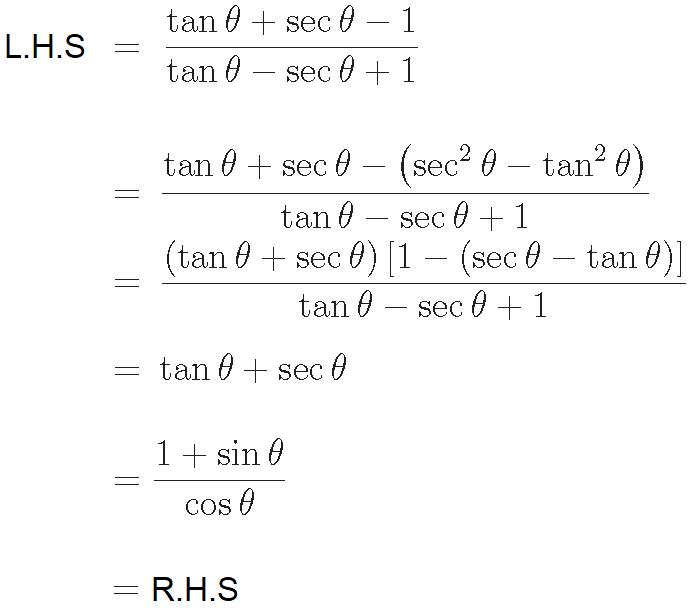
Basic Trigonometric Identities

Trigonometric Identities Examples

How To Solve Trigonometric Identities Newstrack English 1

Solved 4 A Evaluate 27 2 C 1 Dx 1 22 You May Use Chegg Com

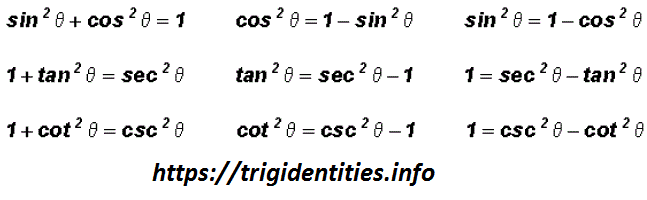
Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities

Solved 2 Prove The Following Trig Identities A Prove T Chegg Com

How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic

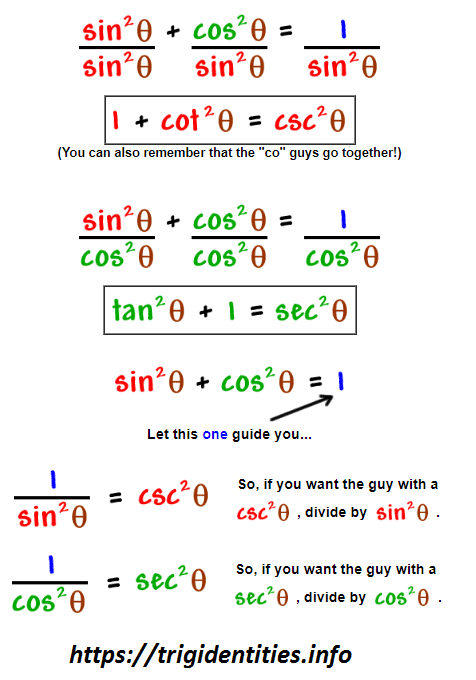
Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities

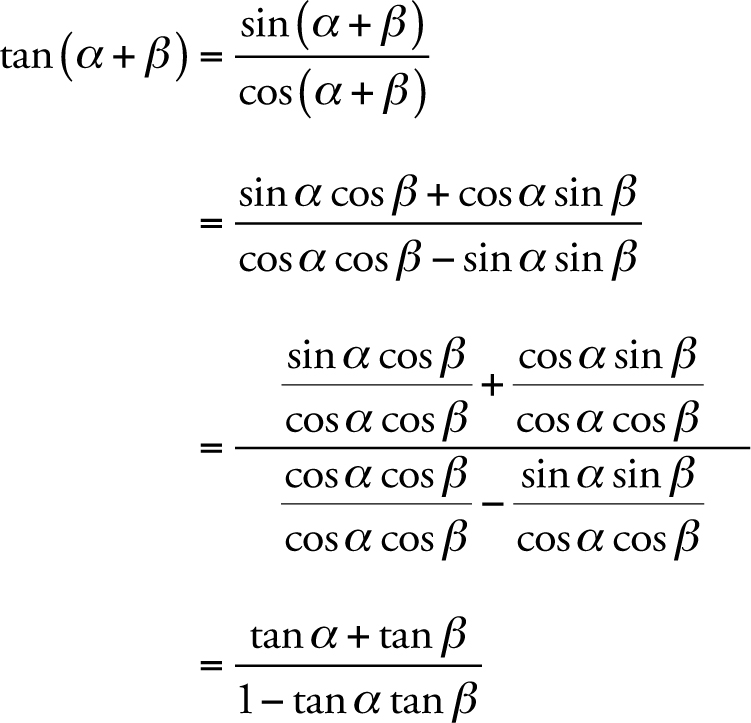
Tangent Identities

Trigonometry Reciprocal Identities Expii

Solved Trig Identities 1 Sin Cos 2 Sin Cos 2 2 2 Tan2 Cos2 Cot2 Sin2 1 3 Sec Course Hero

Trigonometric Identities List Of Trigonometric Identities Examples

Tangent Half Angle Formula Wikipedia

How Do You Use The Fundamental Trigonometric Identities To Determine The Simplified Form Of The Expression Socratic

7 Proving Ids Trig Functions Identities

Summary Of Trigonometric Identities

Solved Establish The Identity 1 Tan 2 Theta 1 Tan 2 Chegg Com

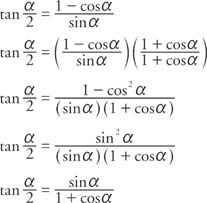
Tangent Identities

Verifying Trigonometric Identities Process Make One Side Look

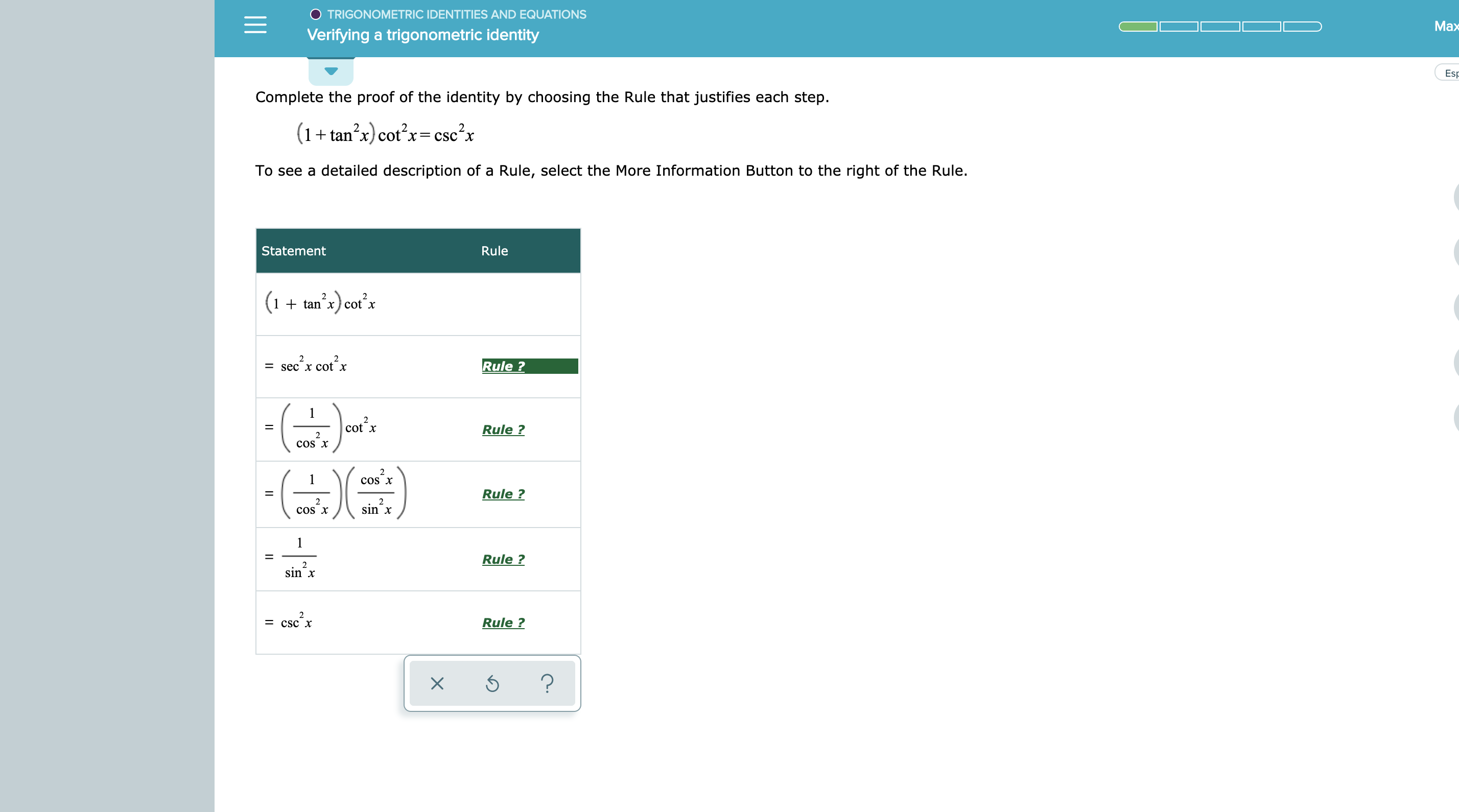
Answered Trigonometric Identities And Equations Bartleby

Every Day I M Calculatin I D3 Unit Q Pythagorean Identities

Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions

Trigonometric Identities List Of Trigonometric Identities Examples

Trigonometric Identities

Integrate Sec 2x Method 2

Tangent Half Angle Formula Wikipedia

Summary Of Trigonometric Identities

What Are The Quotient Identities For A Trigonometric Functions Socratic

14 2 Trigonometric Identities

Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download

Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions

Worksheet On Trigonometric Identities Establishing Identities Hints

Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube

Trig Identities Pdf Trigonometric Identities Fundamental Identities Sin 2 A Cos 2 A 1 1 Tan 2 A Sec 2 A 1 Cot 2 A Csc 2 A Sin A Sin A Cos A Cos A Tan Course Hero

Solved 2 Prove The Following Trig Identities A Prove Chegg Com

Trigonometric Identities Topics In Trigonometry

Incoming Term: trigonometric identities tan^2, trig identities tan^2 theta,